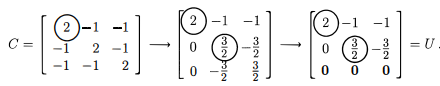[기초계산수학] 1.3 Elimination Leads to K = LDLᵀ

시작에 앞서..

이 포스팅 시리즈는 대학원 수업 [기초계산수학]의 내용을 바탕으로 정리한 글입니다. Gilbert strang 교수님의 책 “Computational science and engineering¹“을 참고하여 작성하였습니다.

1. Gaussian Elimination과 LU Factorization

선형 방정식 시스템을 푸는 가장 보편적인 방법은 가우스 소거법(Gaussian elimination)이다. 이 방법은 행렬을 하삼각 행렬 $L$과 상삼각 행렬 $U$로 분해하는 LU 분해를 이용한다.

\[K u = f\]

소거법은 결정식이나 크래머의 규칙과는 달리 직접적이며 빠르기 때문에 현대의 모든 소프트웨어 패키지가 이를 사용한다.

2. LU 분해를 통한 방정식 풀이 예제

다음과 같은 3×3 행렬 방정식을 생각해보자.

\[K = \begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{bmatrix}, \quad f = \begin{bmatrix}4 \\ 0 \\ 0\end{bmatrix}\]

이를 행 연산으로 상삼각 형태로 변형하면 다음과 같은 결과를 얻는다.

\[U = \begin{bmatrix} 2 & -1 & 0 \\ 0 & \frac{3}{2} & -1 \\ 0 & 0 & \frac{4}{3} \end{bmatrix}\]

이후 back substitution을 통해 해를 쉽게 찾을 수 있다.

• 마지막 방정식에서 $ u_3 = 1 $.
• 두 번째 방정식에 대입하면 $ u_2 = 2 $.
• 첫 번째 방정식에서 $ u_1 = 3 $.

따라서 해는 $ u = (3, 2, 1) $ 이다.

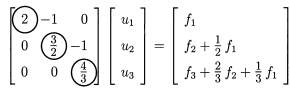Fig 1 - Gaussian elimination을 통한 행렬 $K$의 $U$ 변형 과정

3. 역행렬의 의미와 활용

행렬 방정식 $ K u = f $의 해를 찾는 것은 곧 벡터 $ f $를 행렬 $ K $의 열 벡터들의 선형 결합으로 표현하는 것이다.

즉, \(K u = u_1(\text{col 1}) + u_2(\text{col 2}) + u_3(\text{col 3}) = f\)

행렬 $K$가 가역(invertible)이라면 역행렬 $K^{-1}$의 첫 번째 열은 위에서 찾은 해 벡터 $u$를 $f$의 첫 성분으로 나눈 값과 같다.

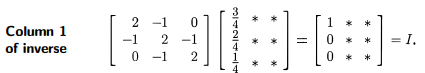Fig 2 - 역행렬 $K^{-1}$의 첫 번째 열을 구하는 과정

4. LU 분해에서의 multiplier 개념

가우스 소거법에서 각 단계의 multiplier $\ell_{ij}$는 다음과 같다: \(\ell_{ij} = \frac{\text{제거할 행(i)의 원소}}{\text{피벗 행(j)의 피벗}}\)

이를 사용하여 하삼각행렬 $L$과 상삼각행렬 $U$를 구성할 수 있다. $L$은 diagonal 원소가 1이고, 아래 삼각 부분은 multiplier들로 채워진다.

예제의 $K$에 대한 LU 분해 결과: \(K = LU = \begin{bmatrix} 1 & 0 & 0 \\ -\frac{1}{2} & 1 & 0 \\ 0 & -\frac{2}{3} & 1 \end{bmatrix} \begin{bmatrix} 2 & -1 & 0 \\ 0 & \frac{3}{2} & -1 \\ 0 & 0 & \frac{4}{3} \end{bmatrix}\)

5. 특이행렬(Singular Matrix)

피벗 과정에서 피벗이 0이 되면 그 행렬은 특이행렬(singular matrix)이 되어 역행렬이 존재하지 않는다. 이때 행 교환(row exchange)을 통해 피벗을 찾을 수도 있다. 행 교환이 불가능하면 행렬은 최종적으로 특이행렬로 판정된다.

특이행렬의 예시 행렬 $C$: \(C = \begin{bmatrix} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{bmatrix}\)

위 행렬은 소거 과정에서 마지막 행의 피벗이 0이 되어 특이행렬이 됨이 드러난다.

Fig 3 - 특이행렬 판정 예제

6. 행 교환이 필요한 비특이행렬

피벗 위치에 0이 있더라도 그 아래에 0이 아닌 원소가 존재하면 행 교환을 통해 소거법을 계속할 수 있다. 행 교환은 순열 행렬(permutation matrix) $P$를 통해 표현할 수 있으며, 이때 최종 분해는 $PA=LU$ 형태로 나타난다.

7. 행 교환과 LU 분해의 세 가지 가능성

가우스 소거법에서 행 교환(row exchanges)을 고려하면 다음 세 가지 가능성이 있다:

1. 행 교환 없이 $ n $개의 피벗을 얻음:
   → 행렬 $ A $는 가역이며, $ A = LU $.

2. 행 교환을 통해 $ n $개의 피벗을 얻음:
   → 행렬 $ A $는 가역이며, $ PA = LU $ ($P$는 순열 행렬).

3. $ n $개의 피벗을 얻을 수 없음:
   → 행렬 $ A $는 특이행렬이며, 역행렬이 존재하지 않음.

8. 대칭행렬과 LDLᵀ 분해

가우스 소거법에서 얻어진 LU 분해는 일반적으로 원 행렬의 대칭성을 유지하지 못한다. 그러나 원래 행렬 $ K $가 대칭행렬인 경우, 다음과 같이 LDLᵀ 분해로 변형하면 대칭성을 유지할 수 있다:

\[K = LDL^T\]

여기서 $ D $는 피벗(pivot)을 포함한 대각행렬이며, $ L $은 하삼각행렬로 diagonal에 1을 갖는다. 신기하게도 대각행렬은 $ U $ 행렬의 대각 원소만 가져오면 된다.

3×3 예시 행렬의 LDLᵀ 분해는 다음과 같다:

\[K = \begin{bmatrix} 1 & 0 & 0 \\ -\frac{1}{2} & 1 & 0 \\ 0 & -\frac{2}{3} & 1 \end{bmatrix} \begin{bmatrix} 2 & 0 & 0 \\ 0 & \frac{3}{2} & 0 \\ 0 & 0 & \frac{4}{3} \end{bmatrix} \begin{bmatrix} 1 & -\frac{1}{2} & 0 \\ 0 & 1 & -\frac{2}{3} \\ 0 & 0 & 1 \end{bmatrix}\]

9. $ A^TCA $ 형태의 행렬의 대칭성

일반적으로 행렬의 곱 형태 $A^T C A$에서 $C$가 대칭 행렬이면, 결과 행렬 역시 항상 대칭 행렬이 된다:

• 특별한 경우로 $C=I$일 때, $A^T A$는 항상 대칭 행렬이다.
• 이러한 형태의 행렬은 수치계산에서 빈번히 등장하며, 추가 조건을 만족하면 양의 정부호(positive definite)가 된다.

10. 행렬 $ K_n $의 determinant

행렬 $ K_n $의 LU 분해를 이용하면 determinant를 간편히 구할 수 있다:

• determinant는 모든 피벗의 곱이다.
• 삼중대각(tridiagonal) 행렬 $ K_n $의 경우 $n+1$이라는 간단한 결과가 나타난다:

\[\text{det}(K_n) = n+1\]

11. Tridiagonal 행렬에서의 피벗과 multiplier의 패턴

삼중대각(tridiagonal) 행렬의 피벗과 multiplier는 일정한 패턴을 보인다.

• $ i $번째 피벗: \(\frac{i+1}{i}\)

• multiplier는 다음과 같다: \(\ell_{i,i-1} = -\frac{i-1}{i}\)

이때 $ L, U $는 bidiagonal 형태를 유지한다. 이는 계산량 측면에서 매우 효율적이다.

12. 양의 정부호 행렬(Positive Definite Matrix)의 판정

대칭 행렬이 양의 정부호(positive definite)이기 위한 조건은 다음과 같다:

• 모든 피벗이 양수여야 한다.
• 피벗 위치에 0이 나타나지 않으며, 행 교환을 필요로 하지 않는다.

2×2 행렬의 예시로 살펴보면:

\[\begin{bmatrix} a & b \\ b & c \end{bmatrix}\]

다음 두 조건이 모두 만족되면 양의 정부호 행렬이다:

1. $ a > 0 $
2. $ ac - b^2 > 0 $

13. Positive definite 행렬의 피벗과 상단 왼쪽 부분 행렬의 determinant 관계

Positive definite 행렬의 피벗과 행렬의 상단 왼쪽 부분 행렬의 determinant 사이에는 중요한 관계가 존재한다:

• 행렬 $K$의 모든 upper-left determinants(상단 왼쪽 행렬식)는 양수여야 하며, 이는 모든 피벗이 양수인 조건과 일치한다.

예시로 3×3 행렬 $ K_3 $의 상단 왼쪽 행렬식은 각각 $2, 3, 4$이며 피벗은 이 행렬식의 비율로 각각 $2, \frac{3}{2}, \frac{4}{3}$가 된다.

---

Reference

1. Gilbert Strang, Computational Science and Engineering, Wellesley-Cambridge Press, 2007. DOI: 10.1137/1.9780961408817. ↩︎