[기초계산수학] 1.2 Differences, Derivatives, Boundary condtions

시작에 앞서..

이 포스팅 시리즈는 대학원 수업 [기초계산수학]의 내용을 바탕으로 정리한 글입니다. Gilbert strang 교수님의 책 “Computational science and engineering¹“을 참고하여 작성하였습니다.

1. 연속 방정식을 이산 시스템으로 바꾸는 관점

이 장에서는 다음과 같은 고전적인 연속 경계값 문제를 다룬다.

\[- \frac{d^2 u}{dx^2} = f(x), \quad u(0) = u(1) = 0\]

이 식은 공간상에서 두 번 미분된 함수 $ u(x) $ 가 주어진 $ f(x) $ 를 생성하도록 만드는 연속 미분 방정식이다. 이 식을 직접 해석적으로 풀 수도 있지만, 컴퓨터 기반의 수치 계산에서는 이를 유한 차분 방식(finite difference method) 으로 변환해 푼다.

그 결과 이 문제는 다음과 같은 선형 시스템 $ Ku = f $ 으로 바뀐다. 여기서 $ K $ 는 이산 라플라시안(discrete Laplacian) 연산을 수행하는 행렬이며, 경계 조건에 따라 이전 장에서 공부했던 행렬들($ K_n, T_n, B_n $ 등)을을 갖는다.

2. 1차 도함수의 차분 근사

연속 함수의 도함수 $ u’(x) $ 를 수치적으로 계산하기 위해 가장 기본적인 접근은 유한 차분(finite difference) 이다. 미분의 정의 자체가 극한으로부터 유도되기 때문에, 적절히 작은 $ h $ 를 선택해 다음과 같은 근사식들을 사용할 수 있다.

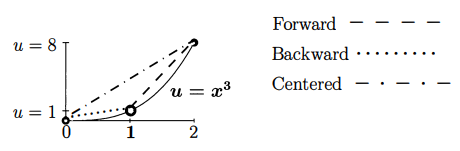
2.1 순방향 차분 (Forward Difference)

\[\frac{u(x+h) - u(x)}{h}\]

이 근사는 다음과 같은 테일러 전개로 표현할 수 있다.

\[= u'(x) + \frac{h}{2} u''(x) + \frac{h^2}{6} u'''(x) + \cdots\]

즉, 오차 항은 $ O(h) $ 이다. $ h \to 0 $ 이면 정확하지만, 실제 계산에서는 $ h $ 가 유한하므로 오차가 남는다.

2.2 역방향 차분 (Backward Difference)

\[\frac{u(x) - u(x - h)}{h} = u'(x) - \frac{h}{2} u''(x) + \cdots\]

순방향과 마찬가지로 1차 정확도 $ O(h) $ 를 갖는다.

2.3 중앙 차분 (Centered Difference)

\[\frac{u(x + h) - u(x - h)}{2h}\]

이 방식은 양쪽으로부터 값을 취하므로 보다 균형 잡힌 근사다. 테일러 전개하면:

\[= u'(x) + \frac{h^2}{6} u'''(x) + \cdots\]

즉, 오차가 $ O(h^2) $ 이며, 앞의 두 방법보다 정확도가 더 높다.

Fig 1 - 도함수의 세 가지 유한 차분 근사 방식

3. 2차 도함수의 중심 차분 근사

2계 미분인 $ u''(x) $ 도 마찬가지로 유한 차분으로 근사할 수 있다.
중앙 차분 방식은 다음과 같다.

\[\frac{u(x+h) - 2u(x) + u(x-h)}{h^2}\]

이 식은 정확도 $ O(h^2) $ 를 가진다. 이는 $ u(x) = x^2 $ 같은 2차 다항식에 대해 정확하게 일치한다. 차분 연산을 벡터에 적용하면, 이를 행렬로 나타낼 수 있다. $ n $ 개의 내부 격자점이 있을 때, 해당 차분 행렬은 다음과 같은 구조를 갖는다:

\[K_n = \begin{bmatrix} 2 & -1 & 0 & \cdots & 0 \\ -1 & 2 & -1 & \cdots & 0 \\ 0 & -1 & 2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & -1 \\ 0 & 0 & 0 & -1 & 2 \end{bmatrix}\]

이건?! 맞다. 이전 장에서 배웠던 $K$ 행렬이다. 이 행렬은 이산 라플라시안(discrete Laplacian) 을 나타내며, 2차 미분을 수행하는 행렬이다.

4. 다양한 입력 벡터에 대한 차분 작용

차분 행렬이 어떤 연산을 수행하는지를 확인하기 위해, 입력 벡터 $ u $ 를 다양한 형태로 설정하고 $ Ku $ 를 계산할 수 있다.

• 상수 벡터 $ u = [1, 1, …, 1]^T $
  → $ Ku = 0 $
  → 상수 함수의 도함수는 0

• 선형 벡터 $ u_i = i $
  → $ Ku = 0 $
  → 1차 함수의 2계 미분은 0

• 2차 벡터 $ u_i = i^2 $
  → $ Ku = \text{상수 벡터} $
  → 2차 함수는 2계 미분 시 상수

• 램프 벡터 (ReLU라고 생각해도 될듯)
  → $ Ku $ 는 특정 지점에서 급격히 튀는 디랙 델타 ($ \delta(x - \alpha) $) 형태

• 사인, 코사인 또는 복소 지수 함수
  → $ Ku = \lambda u $, 즉 고유값 문제

이 결과는 차분 행렬이 고유벡터(사인, 복소지수) 에 대해 스케일만 바꾸는 작용을 한다는 것을 보여준다.

5. 주기 함수 입력에 대한 고유값 계산

입력 벡터로 주기 함수를 취했을 때, $ Ku = \lambda u $ 의 형태로 결과가 나온다. 이때 고유값은 다음과 같이 주어진다:

\[\lambda(t) = 2\cos(t) - 2\]

이 결과는 이산 푸리에 변환(DFT)에서 등장하는 푸리에 고유값 구조와 일치한다.

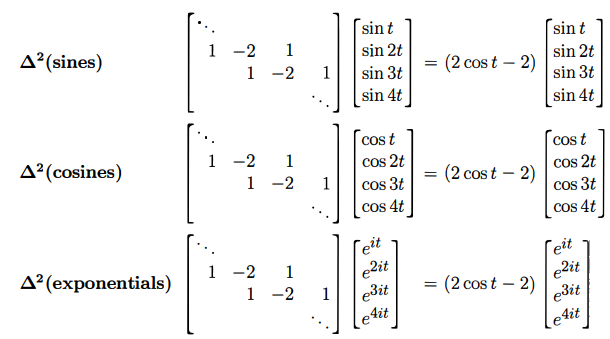Fig 2 - sin, cos, exp 함수 입력에 대한 고유값 계산 결과

6. 미분 방정식의 이산화: 행렬 방정식 $ Ku = f $

연속 문제

\[- \frac{d^2 u}{dx^2} = f(x), \quad u(0) = u(1) = 0\]

를 $ n $ 개의 내부 격자점으로 이산화하면, 해의 근사값을 담은 벡터 $ u = [u_1, u_2, \dots, u_n]^T $ 와 함께 다음과 같은 행렬 방정식으로 바뀐다.

\[\frac{1}{h^2} K_n u = f\]

여기서 $ h = \frac{1}{n+1} $ 는 격자 간격이며, $ K_n $ 은 앞서 설명한 삼중 대각 행렬이다. 우변 $ f $ 역시 $ f_1, f_2, \dots, f_n $ 값으로 구성된 벡터다.

이 시스템은 선형 방정식이며, 수치적으로 직접 풀 수 있다. 중요한 점은 이 행렬이 희소(sparse) 하고 대칭(symmetric) 이며, 양의 정부호(positive definite) 라는 점이다.

Fig 3 - $ u = [u_1, u_2, \dots, u_n]^T $ 해의 근사

7. 경계 조건이 행렬을 결정한다

경계 조건은 단지 수식의 추가 요소가 아니라, 해를 정의하는 데 필수적인 정보다. 수치적으로는 경계 조건이 차분 행렬의 구조를 변경한다.

• 고정–고정: $ K_n $ 사용
• 자유–고정: $ T_n $ 사용
• 자유–자유: $ B_n $ 사용 (마지막 행도 변경됨)

이는 곧, 같은 미분 방정식이라도 어떤 경계 조건을 적용하는지에 따라 해의 구조와 수치적 안정성이 크게 달라진다는 것을 의미한다.

8. 중심 차분을 사용한 경계 조건 근사의 정확도 향상

자유 경계 조건 $ u’(0) = 0 $ 을 $ \frac{u_1 - u_0}{h} = 0 $ 로 근사하면 1차 정확도를 갖는다. 그러나 다음과 같이 중심 차분(centered difference) 를 사용하면 더 높은 정확도를 얻을 수 있다.

\[\frac{u_1 - u_{-1}}{2h} = 0 \Rightarrow u_{-1} = u_1\]

이 식을 이용하면, 다음과 같은 수정이 가능하다:

\[u_0 - u_1 = \frac{1}{2} h^2 f(0)\]

이는 정확도 $ O(h^2) $ 를 가지며, 전체 해의 품질을 향상시킨다. 경계 조건은 단순히 한 줄의 수식이 아니라, 전체 문제의 정확도에 본질적인 영향을 미친다.

9. 결론

• 연속적인 2계 미분 방정식은 유한 차분을 통해 이산화될 수 있으며, 이는 희소하고 대칭적인 행렬 방정식으로 표현된다.
• 중심 차분은 높은 정확도를 제공하고, 사인·지수 함수 등은 이산 라플라시안 행렬의 고유벡터가 된다.
• 경계 조건은 차분 행렬의 형태를 결정하며, 해의 존재성과 유일성, 그리고 수치적 정확도에 직접적인 영향을 미친다.
• 특히 경계에서의 차분 방법(일방향 vs 중심 차분)은 전체 해의 정확도를 좌우한다. 이를 정교하게 처리하는 것이 고정밀 수치 해석의 핵심이다.

---

Reference

1. Gilbert Strang, Computational Science and Engineering, Wellesley-Cambridge Press, 2007. DOI: 10.1137/1.9780961408817. ↩︎